Programmieren lernen mit Etoys
Etoys ist eine Programmierumgebung,
die weitgehend ohne die Eingabe von Quelltexten auskommt. Sie basiert
auf Squeak, einer grafischen
Entwicklungsumgebung für Smalltalk. Man merkt Etoys die Nähe zu
Smalltalk an: alles ist ein Objekt. Darüber hinaus bereitet Etoys
hauptsächlich Spaß. Es macht einfach Freude, mit den vorgefertigten
Komponenten zu spielen oder …
Tastatur Hacking
Tastaturen sind langweilig. Tastaturen sind langweilig? Keineswegs.
Wenn du sie aufschraubst und das Innenleben auf kreative Weise neu
verwendest, nennt man das Hardware Hacking. Und genau das mache ich in
einem kleinen Workshop: Du wirst eine Tastatur auseinander bauen und
den Controller, der die Tasten über den USB-Anschluss an den …
Android Programmierung
Mit Hilfe des AppInventors vom MIT lassen sich auch ohne Programmierkenntnisse mit geringem Aufwand schnell und einfach Apps für Android-Geräte erstellen. In einem kleinen Skript habe ich die ersten Schritte zusammengestellt.
Update: Das Skript wurde heute (8.10.) aktualisiert und etwas aufgeräumt. Über Hinweise freue ich mich …
more ...Tweets des Monats Juli
- Wer an saubere olympische Spiele glaubt, sollte sich nicht anhören, was Werner Franke zum Thema Doping sagt. http://t.co/OgtoMGCM
- Der Spieleklassiker "Giana Sisters" soll neu aufgelegt werden - wieder mit Musik von Chris Hülsbeck. http://t.co/EGErGuVS** **
- Arthur Benjamin erklärt: Statistik ist für unsere Schüler wichtiger als Analysis …
Warum "Minus mal Minus" als Ergebnis Plus ergibt
Jeder hat es in seiner Schulzeit gelernt: Wenn zwei negative Zahlen miteinander multipliziert werden, ist das Ergebnis positiv: (‒2) ∙ (‒6) = 12. Aber warum eigentlich?
Guillermo Bautista hat es in einem Blogartikel verständlich beschrieben.
Nehmen wir einfach einmal an, dass das Produkt zweier negativer Zahlen nicht positiv, sondern negativ sei. Geht …
more ...> Ein Einstieg in Textadventures
Das alte aber keineswegs angestaubte Computerspielgenre der
Textadventures - im Englischen als Interactive Fiction (kurz IF)
bezeichnet - hat es nicht leicht. Kommt es doch mit viel Text, wenig
bis gar keiner Grafik und keinem Sound daher. Was spricht also dafür,
sich ein so "langweiliges" Genre genauer anzuschauen?
Ganz einfach: Es kann …
Flipped Classroom: Den Unterricht auf den Kopf stellen
Derzeit probiere ich das Konzept des flipped classroom aus. Kurz
zusammengefasst wird hierbei das Lernen in die Hausaufgaben verlagert
und der Unterricht in der Schule für Übungen und Anwendungsaufgaben
genutzt.
Für die Videos kann man auf zahlreiche Quellen bei YouTube
zurückgreifen oder selbst ein Video erstellen. Ich habe bisher zwei …
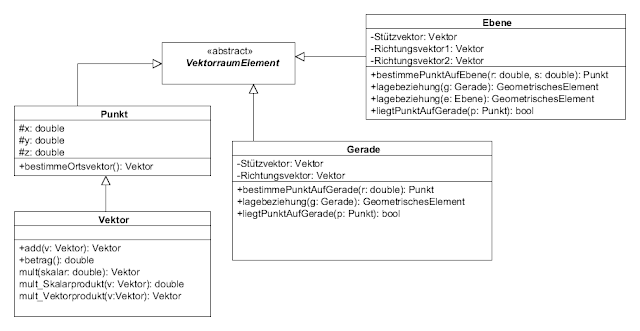
Arbeitsblatt zum Thema Vererbung
Ich habe ein Arbeitsblatt zum Thema
Vererbung in
der Objekt-Orientierten Programmierung (OOP) erstellt. Es geht um die
UML-Notation in Klassendiagrammen und die zugehörige Implementierung
in C# (sollte aber auch für Java funktionieren bzw. sich leicht
anpassen lassen).
Ich freue mich über eure Rückmeldungen.
Vektorrechnung für Programmierer
buch
bildung
Tools
hardware
Comic
Taschenrechner
Funktionen
lernen
wiki
server
Tipp
Linux
raspberrypi
Geschichten
admin
podcast
review
HP35s
Mathe
Informatik
software
video
Gesellschaft
ctf
mooc
git
Spiele
TV
ldl
python
Datenbank
Bilder
Chat
Termin
cloud
gamejam
Second Life
das-labor
Kino
importiert
programmierung
35c3
Windows
screencast
esp8266
39c3
Studium
Linkliste
Spaß
ldlmooc
e-mail
Latex
Clonezilla
audio
Sport
llm
game-engine
Konferenz
Text
RSS
c't
ccc
Tafelbild
JavaScript
kunst
bloggen
hacking
Wissenschaft
film
Twitter
fun
34c3
pdf
Dortmund